第十三届全国研究生数学建模竞赛于2016年9月16日上午8:00开始,2016年9月20日中午12:00结束,整个赛事持续100小时.这是一场数学应用能力的比拼,更是一场团队合作和身体体能的考验.期间很多小伙伴向我咨询一些问题,涉及到题目内容的理解,方法的选择,求解技巧等多个方面.为了促进大家的交流,下面简单谈谈我对B题的理解.
申明:本人没有正式参加这次研赛,只是出于兴趣和交流的目的提供本文,以下做法仅仅代表我个人对本题目的理解.
题目背景介绍
这道题目以遗传性疾病为背景,主要研究遗传性疾病和致病基因(位点)的关系,希望参赛人员根据已有数据找出导致疾病形成的主要位点(基因).从现实应用的角度来看,如果能定位与性状或疾病相关联的位点在染色体或基因中的位置,能帮助研究人员了解性状和一些疾病的遗传机理,也能使人们对致病位点加以干预,防止一些遗传病的发生. 竞赛的题目和原始数据请在单击这儿下载。
问题1
请用适当的方法,把genotype.dat中每个位点的碱基(A,T,C,G) 编码方式转化成数值编码方式,便于进行数据分析.
DNA 序列, 由 C、T 、A 、G 四种碱基排列而成. 因此对 4种碱基进行数字编码,可用 0(00)、1(01)、2( 10) 和 3(11) 4 个数字对4种碱基进行编码. 这种编码格式共有 4!=24 种编码方式的组合. 4 个碱基中, C 与 G 互补, T与A互补, 因此,4 种碱基的数字编码, 应满足互补法则. 而4 个数字中 0(00) 与 3( 11) 互补, 1(01) 与 2(10). C、T 、A 、 G 4种碱基满足互补法则的数字编码格式共有 8 种,其余 16 种数字编码格式, 因不满足互补法则而被摒弃. 研究已经表明 C:0 T:1 A:2 G:3 这种按分子量大小顺序排列的编码格式最好. 因此在本实验中对碱基的编码采用这种方式.
因为染色体具有双螺旋结构,所以用两个碱基的组合表示一个位点的信息,这样四种碱基共有16组合方式
然后,我们首先按照上面的碱基编码原则,按照碱基对中碱基的顺序编码
为了方便后面的计算,我们直接将上述二进制的碱基对直接编码为10进制,
这样便完成了碱基字符编码到数据编码的转换工作,下面是 matlab 实现.
首先把 genotype.dat 载入matlab 工作空间,并保存到 genotype 变量中,其size 为 1001×9445. 按照上面的编码规则,可以将其文本碱基对转化为数值,便于后续的数值分析.
|
|
问题2
根据附录中1000个样本在某条有可能致病的染色体片段上的9445个位点的编码信息(见genotype.dat)和样本患有遗传疾病A的信息(见phenotype.txt文件).设计或采用一个方法,找出某种疾病最有可能的一个或几个致病位点,并给出相关的理论依据.
数据理解:
我们把这1000个样本,还有9445个位点的数据 (genotype.dat) 经过第一问的方案可以转化为一个 1000×9445 的矩阵,称做”特征”. 这里1000为数据样本,9445 为特征的维度. 另外这1000个样本的是否具有遗传病A 的信息保留在 (phenotype.txt)文件, 其中1 表示患有,0表示没有患该病. 这个1000x1 的向量我们叫做样本的“标记”.
问题分析:
题目关键是让我们找出是哪些特征(也就是位点)导致了遗传疾病A?这个问题可以转化为:那些特征 (9445 个位点的部分)可以使得对遗传疾病A有较好的诊断率,那么这些位点肯定和遗传病A有密切关系. 因此这个问题转化为一个特征选择的问题,也就是找出一些特征,使得对遗传疾病A 的诊断有较高的识别率.
方法方案:
涉及识别,也就是分类,SVM 是一种非常经典的统计学习方法,而线性模型的系数恰好可以度量每个特征对分类超平面的贡献.因此我们采用线性SVM,通过求解其系数来确定每个特征贡献.
求解实现:
LIBSVM 和 LIBLINEAR 是非常出名的SVM 求解软件包,它提供了非常丰富的外部接口(例如:matlab,python,java等). 相比于 LIBSVM, LIBLINEAR 主要是线性 SVM 模型,更擅长对高维度数据的求解,因此我们选择 LIBLINEAR 包.
Matlab代码:
step1: 下载最新版的 LIBLINEAR 源程序,编译后加载到 matlab 搜索的路径
step2: 载入编码好的位点特征
step3: 数据标准化
step4: 训练线性SVM 模型
step5: 模型权重的可视化
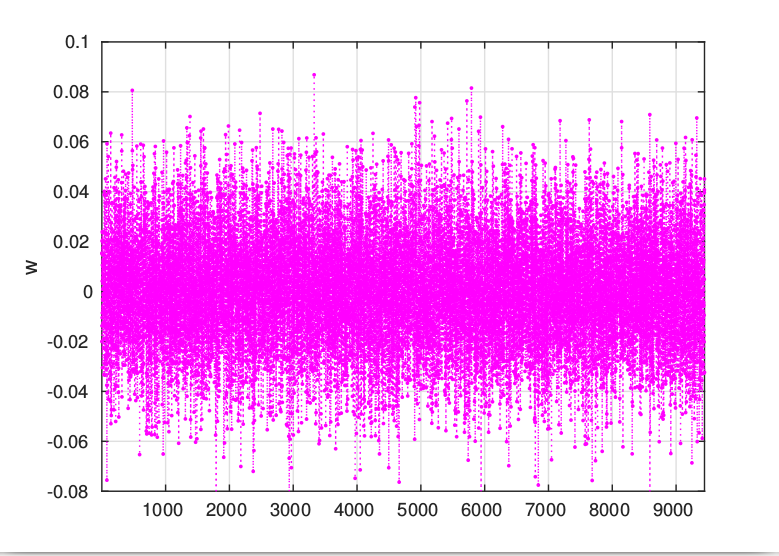
step5: 根据权重绝对值的大小排序,依据此排序选择特征,训练SVM,观察选择特征对其识别性能的影响
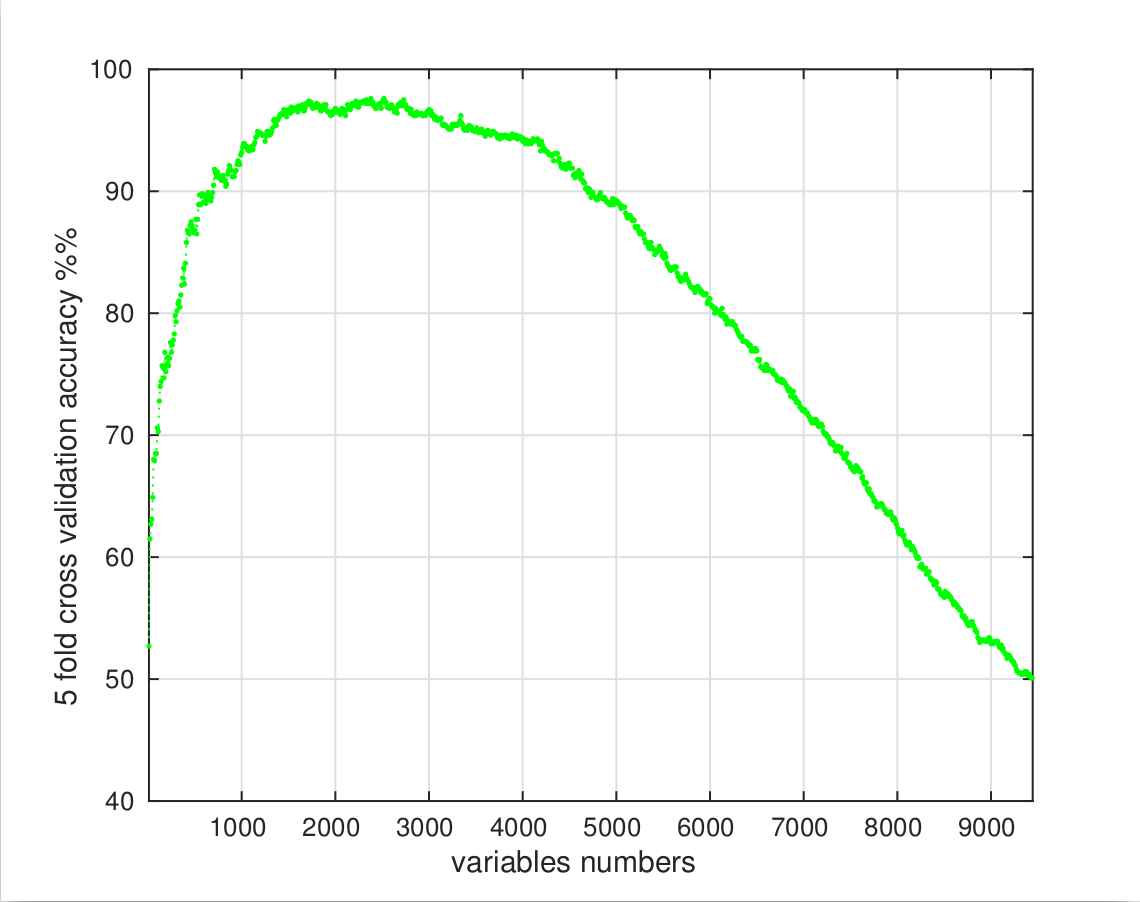
step6: 模型评价,前2450个位点,5-fold 交叉验证识别准确率可以达到98.2%

step7: 输出Top20 的位点
问题3
同上题中的样本患有遗传疾病A的信息(phenotype.txt文件).现有300个基因,每个基因所包含的位点名称见文件夹gene_info中的300个dat文件,每个dat文件列出了对应基因所包含的位点(位点信息见文件genotype.dat).由于可以把基因理解为若干个位点组成的集合,遗传疾病与基因的关联性可以由基因中包含的位点的全集或其子集合表现出来请找出与疾病最有可能相关的一个或几个基因,并说明理由.
问题4
在问题二中,已知9445个位点,其编码信息见genotype.dat文件.在实际的研究中,科研人员往往把相关的性状或疾病看成一个整体,然后来探寻与它们相关的位点或基因.试根据multi_phenos.txt文件给出的1000个样本的10个相关联性状的信息及其9445个位点的编码信息(见genotype.dat),找出与multi_phenos.txt中10个性状有关联的位点.
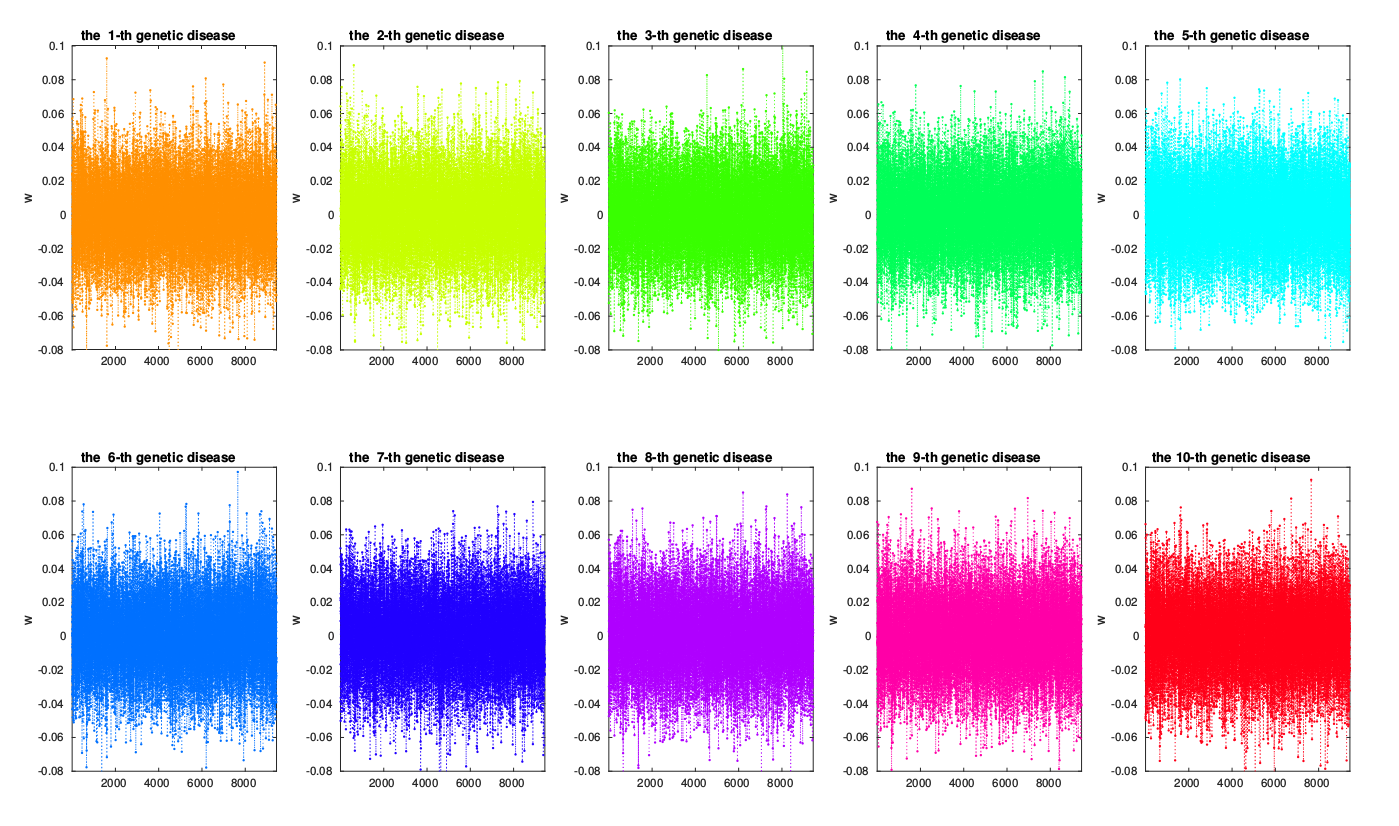
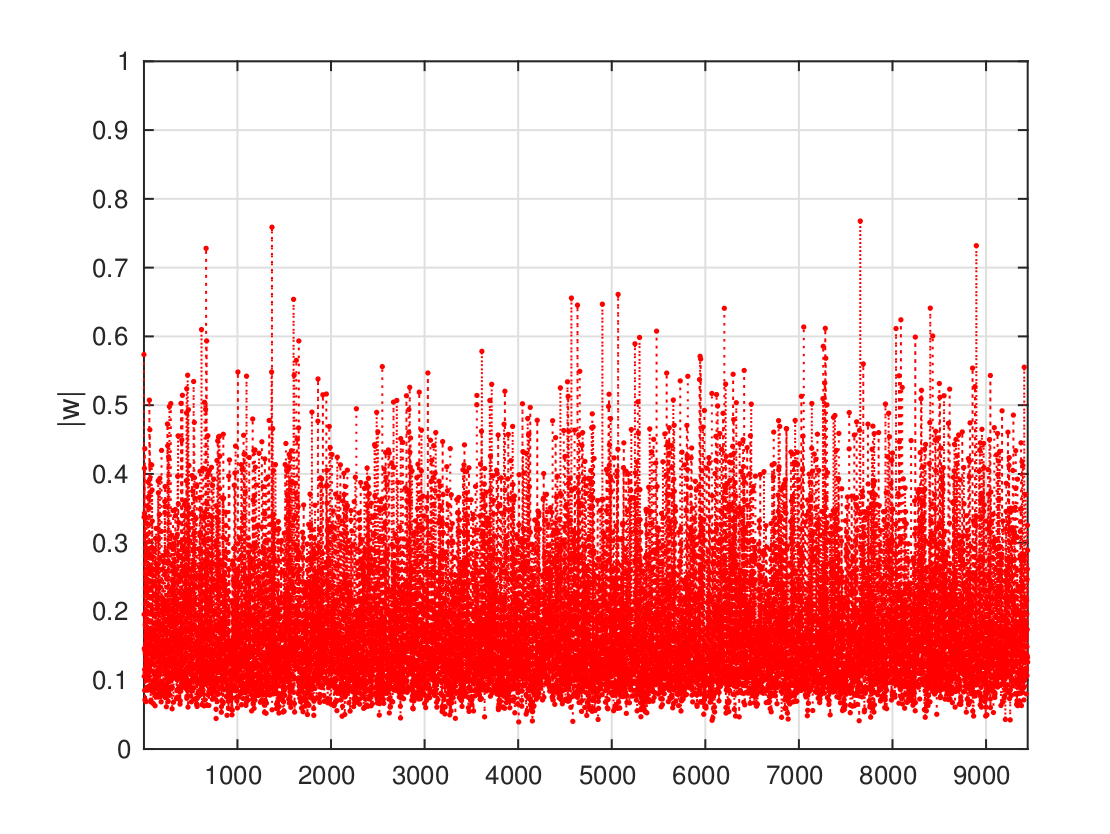
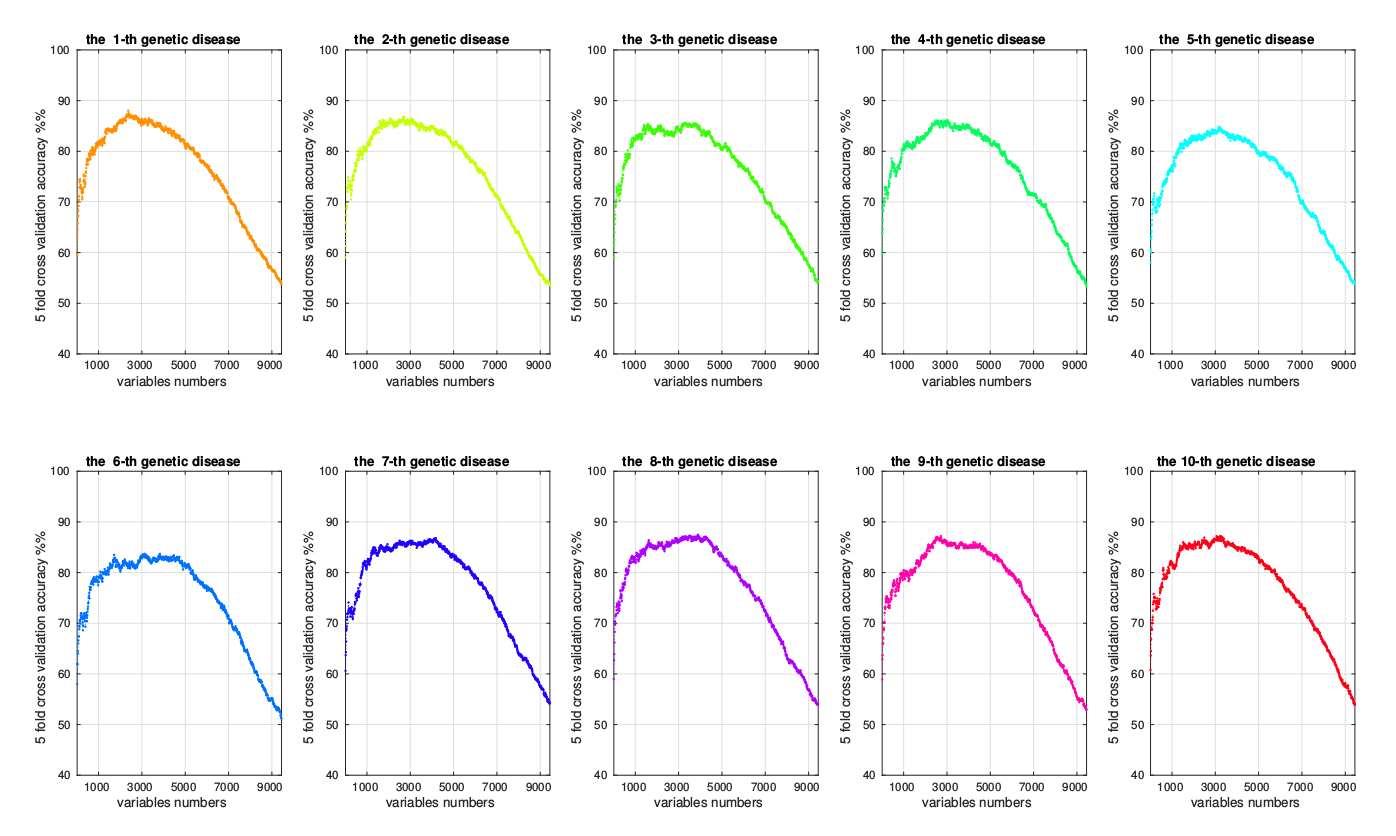
问题 3 和 问题 4 的方案和代码等我抽空在补充完整!
最近访客

本文链接:http://gaobb.github.io/2016/09/20/数学建模_遗传性疾病和性状基因的定位分析/

